要約 – Design Wave Magazine設計コンテスト2008のRSA暗号回路設計結果を報告する．本稿はモンゴメリ乗算アルゴリズムを用いる累乗計算で，RSA暗号処理の中間演算の法を暗号処理で与えられた法Mの3倍にとることでより簡易な回路構成となることを示す．これを回路化するときに，メッセージのビット長Nに回路規模と遅延時間が依存しない回路構成として，冗長表現を用いたビットシリアル演算回路を用いた．Xilinx社のSparntan3をターゲットに合成をおこない，50入力 XORに対して回路規模47倍，遅延時間1.8の結果を得た．さらにスループットを2倍にする方法として，本稿の基数2の設計に対して基数4で設計した場合を取り上げ，そのメリットを回路規模と遅延時間から考察をした．

Keywords – RSA暗号処理，モンゴメリ乗算

I. RSA暗号のなかみ

RSA暗号処理をまとめます．平文Cp，暗号文Ce，暗号化鍵E，復号鍵D,および法Mがそれぞれ正整数で与えられているときに，以下の式を用いて暗号化をおこないます．

--- (1)

ここでmodは剰余を求める演算子で，A mod BはAをBで割った余りをあらわします．RSA暗号は以下の式を用いて復号を行います．

--- (2)

RSA暗号の暗号化と復号処理はいずれも，累乗の剰余で与えられます．

暗号化鍵E，復号鍵Dおよび法Mそれぞれは以下の条件を満たすように選びます． まず法Mは十分大きな2つの素数pおよびqの積で与えます．このとき(p-1)および(q-1)の最小公倍数をLとすれば，

--- (3)

が成り立ちます．したがって暗号化鍵Eおよび復号鍵Dを正の整数をHとして，

--- (4)

を満たすように決めます．つまり，RSA暗号は剰余演算の累乗の周期を利用した暗号アルゴリズムというわけです．

RSA暗号では，送信者は受信者から渡された法Mおよび暗号化鍵 Eから式(1)で平文から暗号文を求めます．受信者は法Mおよび秘密にしている復号鍵 Dから式(2)で暗号文から平文を復号します．

II. 回路化に適したアルゴリズムを考える

これでRSA暗号化器の設計は，式(1)の法Mの剰余で累乗を計算する回路の設計だと分かります．この剰余の四則演算を剰余演算と呼ぶことにします．回路化するために本稿で取った余剰演算のテクニックを述べます．

説明のために暗号化鍵E，復号鍵Dを正整数N として2進数で表されるNビットの整数(つまり， (2^N -1) >= E, D >= 0)とします．法Mは最上位ビット(Most Significant Bit, 以下MSb)が’1’のNビットの奇数(十分大きな2つの素数の積は因数2を含まないから奇数になる，また (2^N -1) >=M > (2^N-1 -1))，平文Cpおよび暗号文Ceは法Mより小さい正の整数とします．

もしも平文Cpの剰余計算を，まず通常の四則演算をしてから法Mの剰余を求めたとすればどうでしょうか．通常，ビット長Nには1024ビットという大きな値が取られますから，その乗算結果は2048ビットになります．この数を除算して剰余を求めるとすれば，乗算1回あたり1024ビットの乗算と2048ビットの除算をすることになります．これを素直に回路化すれば大変な回路面積になってしまいます．

(テクニック１，改良モンゴメリ・アルゴリズム)

そこで除算をしなくても剰余演算の乗算ができるモンゴメリ・アルゴリズムによるモンゴメリ乗算回路を採用ました．章IIIに，以下に述べる冗長2進表現に適するようにこのアルゴリズムを改良した点を述べます．

(テクニック2 ，冗長2進表現をとるビット･シリアル演算回路)

乗算回路には必ず加算回路が必要です．1024-bitの加算回路を何も考えずに設計すると桁上げ信号の伝播遅延時間が大きくなり実用的ではありません．そこで1桁の数値を1ビットの0/1ではなく 2ビットで表す冗長2進表現を採用しました．本稿の冗長2進表現は値{0, 1, 2, 3}それぞれに{2’b00, 2’b01, 2’b10, 2’b11}を割りあげます．この冗長表現により桁上げがなくなり高速な加算回路が得られます．加算回路構成は1桁づつ演算をするビット･シリアル演算回路を採用しました．この回路はビット長Nに動作速度が依存しないので，ビット長Nが大きい暗号にも動作速度を落とさずに対応 できるという拡張性が得られます． 章VIに，冗長2進表現のビット･シリアル加算，乗算および自乗回路の構成を述べます．

(テクニック3 ，入出力はすべてLSb-first )

ビット･シリアル演算回路を縦接続するときに，例えば，前段および次段がそれぞれLSb-first出力，MSb-first入力だと，接続部分にMSbとLSbの順序を入れ替えるためにビット長Nのバッファが余分に必要になってしまいます．このビット長Nの順序入れかえはNクロックかかるので処理時間の無駄にもなります．

本稿はLSB-first入力を必要とする改良モンゴメリ･アルゴリズムに合わせて，全回路をLSb-first入力にそろえています．章IVに全体回路構成を示します．

III. 改良モンゴメリ乗算法

改良モンゴメリ乗算アルゴリズムをCライクの表記で図１に示します．

図1. 改良モンゴメリ乗算アルゴリズム

図2. モンゴメリ乗算の計算例

図1のモンゴメリ･アルゴリズムのポイントは，積に定数2^-N をかけることで，除算を使わずに，加算とビットシフトだけで法Mの乗算ができることです．図1の計算例を図2に示します．図1 のP1で AとBはビット長Nなので，その積のCはビット長2Nになります．これに2^-Nをかけるので，RはCの上位NビットC₁と，下位NビットC₀と2-^Nの積の合計値になります．

このC₀と2-^Nの積を求めるのが図1のP2になります．まずはC₀ * 2^-1を求めます(図2)．C₀ が偶数であればLSbは’0’なので1-bit右シフトするだけです．C₀ が奇数のときは法M(法Mは2つの素数の積なので必ず奇数)を足してLSbを’0’にしてから1-bit右シフトします．こうして得られたC₀ * 2^-1に同じ処理をあと(N-1)回繰り返せば求めるC₀ * 2^-Nが得られます．最後にC1 とC₀ * 2^-Nを足せばRが求まります．

こうして得られたRはビット長(N+1)で，法Mより大きいかもしれません．オリジナルのモンゴメリ･アルゴリズムはRが法Mより小さくなるようにRから法Mを減算します．これにはRと法Mの値比較と減算という計算ステップが必要になります．この改良アルゴリズムはその計算ステップを省略しています．これは法Mではなくて法3*Mで計算していることになります．この改良アルゴリズムによる累乗アルゴリズムを図3に示します．

図3.累乗アルゴリズム

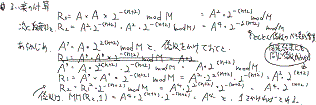図4.乗算により発生する係数の扱い

図3の累乗アルゴリズムそれ自体はよくある累乗アルゴリズムです．2進表記した指数の’0’でない最上位ビットを見つけて，そこから自乗と次のビットが’1’であれば元の値をかけることを繰り返して，求める累乗を得ます．

このアルゴリズムのポイントは，メッセージに定数をかける前処理をしてモンゴメリ乗算で生じる定数をうまく処理すること，および図1のP2のループ回数を(N+2)回にしてモンゴメリ乗算の結果をビット長(N+1)に収めていること，の２つです．

図3の乗算例を図4に示します．

モンゴメリ乗算で単に値Aを自乗するとA²* 2^-(N+2) ，これをさらに自乗するとA⁴* 2^-2(N+2) と自乗するたびに異なる係数がかかります．こうなると自乗するたびに係数2^-(N+2)を取り除かないと正しい結果が得られなくなります．ここで値Aにあらかじめ係数2^2(N+2)をかけておけば，モンゴメリ乗算で自乗を繰り返しても同じ係数2^(N+2) がかかります．この係数2^(N+2) は最後にモンゴメリ乗算で1をかければ取り除けます．

メッセージC_pを前処理した結果得られるR[0]はビット長(N+1)です．図1のP2のループ回数を(N+2)回にすれば自乗した結果はビット長(N+1)に収まります (図5)．

図5.モンゴメリ乗算による累乗計算の桁丸め込み

IV. 回路構成

図6に全体構成を示します． 入出力信号名はコンテスト課題に従います．バス幅の明記がない信号線は全てビット幅1です．インスタンスI0，インスタンスI1は，それぞれ2^(N+2) mod CM を求める回路ブロック，モンゴメリ乗算回路を示します．RSA暗号化処理の手順は以下になります：

1.入力信号をバッファに取り込む．

A) B0,B1およびB2それぞれにブロックサイズ分信号を取り込みます．

2. インスタンスI0で2^(N+2) mod CMを求めます．

3. 図３のメッセージ前処理をおこないます．

A) モンゴメリ乗算回路I1のシリアル入力選択MUX(I2)でI0の出力を選択します．

B) Cp’にはバッファされた平文が取り込まれています．

C) (N+2)サイクル後に出力される乗算結果をバッファB1にバッファします．

4. 累乗計算をおこないます．

A) 図３のR[i]の自乗計算をおこないます．モンゴメリ乗算回路I1を自乗計算に設定してビットシリアル出力をMUX I2でモンゴメリ乗算回路の入力に戻します．

B) 指数CEのMSbの次ビットが’1’ならば，先の乗算結果に前処理した平文Cp’を乗算します．モンゴメリ乗算回路の乗数には手順3-Cで求めた平文Cp’が入力されているので，モンゴメリ乗算回路I1を乗算計算に設定して，計算結果をMUX I1で入力に戻せば，これを求められます．

5. 処理結果をB1に取り込む．

A) 手順3と同じ手順でモンゴメリ乗算回路の出力をバッファB1に取り込む．

6. 処理結果の出力．

A) バッファB1から8ビットづつ選択出力する．

法CMが同じならば手順2の2^(N+2) mod CMの計算を繰り返す必要はありません．ですが設計を簡単にするために毎回これを計算しています．

課題で入出力順序は任意とある入出力信号は，LSB-first, 出力もLSB-firstにしました．またブロックサイズBの値とブロック長の対応は，Bが 0, 1, 2, 3 のときブロック長はそれぞれ1, 2, 3, 4 バイトとしました．

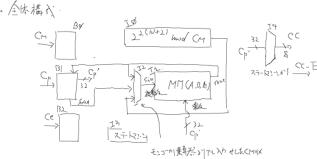
図6. RSA暗号化器 全体回路構成

V. 2^2(N+2)計算回路

2^(N+2) mod Mの計算アルゴリズムを図7に示します．簡単のためにビット長Nを8とします．求める値は9’h100をビットシフトしていくことです．計算結果が法M以下にするため，ビットシフトした結果が法Mより大きければ結果から法を引きます．

図7. 2^2(N+2)の計算アルゴリズム

法Mを引く/引かないの判断は9ビットの値のみで決めます．法Mは2⁸未満の値ですから，9ビット目が’1’であれば必ず法Mが引けます．ただし，計算結果が法2Mより大きい場合があります．このときには法Mを引いても桁上げで9ビット目が再び’1’になりますから，次のサイクルで再度法Mを引きます．9ビット目が’0’ならば右に1ビットシフトして2倍します．これを(N+3)回繰り返せば結果が得られます．

法Mの減算は法Mの2の補数を加算しています．法Mは奇数ですからその補数はビット反転したもののLSbを’0’にするだけで求まります．

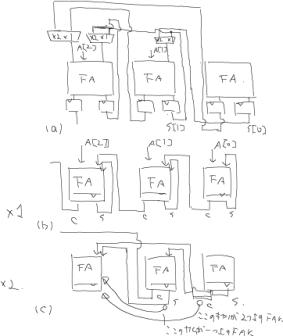
図8.加算器の構成

図7の加算の回路構成を図8に示します．FAは1ビットの全加算器を，下に線が入ったFAは出力がフリップフロップ(以下，F.F.)のFAを示します．桁上げ信号伝播が生じないように，1桁の値をキャリアとサムを組み合わせた2ビットの値(以下，{C, S}と表記します)で表現します．拡張表現{C, S}の (2 * C + S) を求めれば2進数に戻せます．図8(a)の回路は加算と乗算を一度に行います．MUXの働きが分かりにくいので，Aを加算するだけのときの信号配線を図8(b)に示します．キャリアを一段上のFAにサムを同じFAに戻してAを加算します．加算器出力の2倍とAを加算するときの信号配線を図8(c)に示します．キャリアを2段上のFAにサムを1段上のFAに入力します．

図9. 冗長表現の2^2(N+2)計算アルゴリズム

前述のアルゴリズムを拡張表現{C, S}が使えるようにすると図9になります．(N –1)ビット目のキャリアC[N-1]が’1’ならば9ビット目が’1’なので法Mを引きます．(N –1)ビット目のサムS[N-1]が’1’ならば，2倍すると9ビット目が’1’になるので法Mを引きます．ここで，図8から，2倍するとC[N-2]を失うので，C[N-2]が’1’のときには単に1倍してこれを防止しているのがポイントです．拡張表現{C,S}はキャリアとサムを別々に扱うために，それぞれを個別に丁寧に見てやらねば思わぬ計算違いが生じてしまいます．

VI. モンゴメリ乗算回路

モンゴメリ乗算回路の構成を図10に示します．図1のアルゴリズムどおりに，求めた2数の積の下位ビットに2^(N+2)を乗算します．乗算回路を図12および図13に示します．ビットシリアル入力Aと前処理したバッファにあるメッセージBの積は，AのビットとBの部分積を加算していけば求まります．モンゴメリ乗算のビットシリアル出力を入力に戻して直ちに自乗計算するために，自乗回路の部分積は図12に示す順序で入力します．

自乗と乗算を1つの回路で行うように図13の部分積を求める回路を組みました．またブロックサイズに対応するために，ブロックサイズが1, 2, 3, 4それぞれのときに10, 18, 26, 34桁目それぞれのキャリとサムが後段に伝わらないようにMUXを入れています．

図1のC0* 2^-(N+2)を求める回路を図11に示します．2の割り算はビットシフトで実現できます．図1のP2の式P[i+1] = (P[i] + q_i * M + c_i) div 2のLSbの加算をみると入力数が４になります．計算結果が3’b100になるために，結果が冗長表現の1桁{C,S}に収まりません．そこで加算を q_i * M + c_i= q_i * (M –1) + q_i + c_iと分けて別々に加算することで，冗長表現の範囲内に収めます．これを回路にしたのが図11です．法Mは奇数ですから法M のLSbを’0’にすれば(M –1)になります．

ブロックサイズ0~3に対応するために，ブロック数が1, 2, 3, 4 のときにモンゴメリ乗数回路のサイクル数を 10, 18, 26, 34 にそれぞれ設定しています．

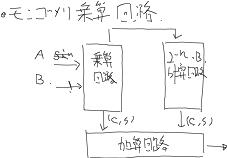
図10.モンゴメリ乗数回路 構成

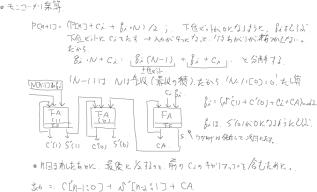
図11. 2^-N乗算回路

図12. ビットシリアル乗算/自乗回路

図13. 部分積回路

VII. 合成結果と考察

Xilinx社のISE version 9.2.03i でターゲットをXC3S50-4(Spartan3 スピードグレード4)として合成した結果を表1に示します．50入力XORの使用スライスおよび遅延時間はそれぞれ10スライスおよび12 nsでした．それらを1単位とした値を括弧内に示しています．

期待値を別プログラムで作成して検証をかけました．全ての入力値に対する検証までは終了しておらず詰めができていません．

表 1 合成結果

項目	値 (50入力 XOR対比)
使用スライス	465 (47)
F.F.の使用数	478
4入力LUTの使用数	849
遅延時間	22.1 ns (1.8)
最大動作クロック	45 MHz

入力信号STARTの立ち上がりから出力信号CC_EN立ち上がりまでのレイテンシは鍵の値によりますが，コンテスト課題の法と復号鍵でのレイテンシを表2にまとめます．

表 2 合成結果

法	復号鍵	レイテンシ
253	61	114 クロック
54991	1657	286クロック
4165512167	612556253	1578 クロック

ターゲットにしたXilinx社のSpartan3は1スライスあたりF.F.とLUTを2つづつ持ちます．合成結果からLUTの数で回路規模(スライス数)が決まったとわかります．今回の設計はビットシリアル演算 で構成しています． したがってLUTの使用数とF.F.の使用数が同数になるように1ビット分演算回路を作りこめば，スライス数は250程度まで絞り込める可能性があります．

動作速度は，モンゴメリ乗算回路の入出力信号の引き回し方法で決まってしまいました．モンゴメリ乗算回路は(N+2)サイクルで計算結果が得られます．その計算結果を次サイクルで直ちにモンゴメリ乗算回路に戻しています．この信号経路は，図14に示すようにモンゴメリ乗算回路の演算回路，LSb加算回路およびMUXを経由するために，遅延時間がかさみました．

これを高速にするには(N+2)サイクルでは加算のみをして，(N+3)サイクル目でモンゴメリ乗算回路に出力結果を戻すようにすればよいです．(N+2)サイクルの最小サイクルで演算することにこだわり設計しましたが，これが(N+3)サイクルになっても，ビット長Nが1024ビット程度であれば全体として0.1%程度処理時間が長くなるに過ぎません．モンゴメリ乗算回路単体は100MHzで動作しますので，処理クロック数が0.1%増えても，100MHzの最大動作速度を狙うべきでした．設計の退くべきところと攻めるところを間違えた，良い教訓を得ました．

図14.モンゴメリ乗算回路まわりのクリティカルパス

VIII. ビット長1024の回路規模と最大動作クロック

本設計はビットシリアル回路構成をとったのでビット長Nを容易に変更できます．大雑把な見積もりかもしれませんが，ビット長32で465スライス使用したので，ビット長1あたりのスライス数は15です．ビット長1024の場合回路規模は15400スライス程度になると予測されます．ビットシリアル回路は動作速度がビット長Nによりませんから，45MHzの動作速度がえられるはずです．

IX. スループットを2倍にする方法，基数を４にする

FPGAでもGbpsレベルの高速シリアル通信が一般になってきています．このような高速シリアル通信に対応するには高いスループットが求められるはずです．スループットを高める今回の設計の改良点を述べます．

スループットを2倍にする手段は基数を2から4にすることです．つまり1クロックあたり1ビット処理していたのを2ビット処理することになります．

回路規模はどの程度になるでしょうか．本設計のほとんどはビットシリアル加算回路が占めています．図15に示すように基数2の加算回路はLUT2つですが，基数4ではLUT7つになります．したがって回路規模は1.8倍程度になると予測されます．また図１のモンゴメリ乗算アルゴリズムに変更が必要です．基数2では最下位桁が0にするためには，法Mを足すか足さないかだけでよかったのですが，基数4では法Mの0, 1, 2, 3 倍のいずれかを足すようにしなければなりません．このために法Mの3倍をあらかじめ求めておくステップと，計算結果を保持するバッファ，それに法Mの倍数を選択するMUXが新たに必要になります．

動作速度は，本設計がそうであったように，1桁の回路動作速度で与えられるとしてよいでしょう．ビット幅が 1ビットから2ビットになってもスライス自体が加算回路に最適化されているSpartan3では，加算回路の動作速度は変わらないと予測されます．基数2の最大クロックは同程度でしょう．

まとめると基数を4にすると回路規模およびスループットは，それぞれ1.8倍，2倍になり，最大動作クロックは基数2とほぼ同じと予測されます．

この結果からレイテンシの短縮が問題になるならば基数を4にする，スループットのみが問題であれば基数を４にするか，もしくは基数2の回路を2つ並列に動作させることが有効だと考えられます．

図15. 基数による加算器の回路規模比較

X. まとめ

改良したモンゴメリ乗算アルゴリズムを用いたRSA暗号化器の設計をおこない回路規模と動作速度の見積もりを得ました．また本設計をビット長1024に適用した場合，および基数を4にした場合の，回路規模と速度を予測しました．

モンゴメリ・アルゴリズムを用いた累乗アルゴリズムで，計算途中結果の法を3Mにとることで， MSb1ビットのみで法Mの減算判定ができて，オリジナルのモンゴメリ乗算アルゴリズムに必要だった法Mの減算判定と減算処理を省略することができました．そのかわりに，オリジナルが乗算1回をNサイクルでできたのに対して，改良アルゴリズムは(N+2) サイクルが必要になりました．しかし，ビット長Nが1024程度の場合，これは0.2％程度のサイクル数の増加にすぎません．

ビット長Nに依存しない前述アルゴリズムの回路化を考えて，ビットシリアル演算回路で構成しました．計算結果のバッファリングおよび前段の計算結果完了待ちサイクルなどの無駄がでないように，全ての演算回路をLSb-first入力，LSb-first出力にして，演算回路間を直接ワイヤ接続できるようにしました．

合成結果は45 MHzとモンゴメリ乗算回路単体の動作速度約100 MHzに及びませんでした．これは(N+2) サイクルで乗算するために演算結果が直ちに演算入力に流れるように設計したパスがクリティカルになったためでした．1サイクル入れて(N+3)サイクルで動かすように設計すれば，モンゴメリ乗算回路単体と同程度の動作クロックになったと思います．サイクル数を(N+2)にする設計にこだわったばかりに最大動作クロックを半分に落としてしまいました．攻めるところと譲るところの見通しが甘かった，いい教訓になりました．

XI. 引用文献

[1] Ching-Chao Yang et. al., “A New RSA Cryptosystem Hardware Design Based on Montgomery’s Algorithm,” IEEE Trans. Circuts and Systems II, vol.45, pp.908-913, July, 1998.

[2] Stephen E. Eldridge and Colin D. Walter, “Hardware Implementation of Montgomery’s Modular Multiplication Algorithm,” IEEE Trans. Comput., vol.42, pp.693-699, June, 1993.